<style>
.layui-table-cell {
height: auto;
overflow: auto;
text-overflow: initial;
white-space: normal;
}
</style>去掉按钮的下边距
.layui-table .layui-btn-container .layui-btn {
margin-bottom: 0;
}
<style>
.layui-table-cell {
height: auto;
overflow: auto;
text-overflow: initial;
white-space: normal;
}
</style>去掉按钮的下边距
.layui-table .layui-btn-container .layui-btn {
margin-bottom: 0;
}
queue:listen 是热加载,效率低,修改job类后会生效
queue:work 不会热加载,效率高,修改job类后需要重启才能生效
https://developer.mozilla.org/zh-CN/docs/Web/API/Clipboard/writeText
function copyText(text) {
if (navigator.clipboard) {
navigator.clipboard.writeText(text).then(
function () {
/* clipboard successfully set */
},
function () {
/* clipboard write failed */
},
);
} else {
let oInput = document.createElement('input');
oInput.value = text;
document.body.appendChild(oInput);
oInput.select();
document.execCommand("Copy");
oInput.className = 'oInput';
oInput.style.display = 'none';
}
}
function oCopy(text) {
copyText(text)
layer.msg('复制成功!')
}配置文件:solrconfig.xml
<requestHandler name="/update" class="solr.UpdateRequestHandler" >
<lst name="defaults">
<str name="update.chain">dedupe</str>
</lst>
</requestHandler>
<updateRequestProcessorChain name="dedupe">
<processor class="solr.processor.SignatureUpdateProcessorFactory">
<bool name="enabled">true</bool>
<str name="signatureField">id</str>
<bool name="overwriteDupes">true</bool>
<str name="fields">object_id,object_type</str>
<str name="signatureClass">solr.processor.Lookup3Signature</str>
</processor>
<processor class="solr.LogUpdateProcessorFactory" />
<processor class="solr.RunUpdateProcessorFactory" />
</updateRequestProcessorChain>修改fields字段为需要去重的字段
docker container run -itd --name solr -e SOLR_JAVA_STACK_SIZE=-Xss1m solr -m 2g指定SOLR_JAVA_STACK_SIZE即可
Starting Solr
Java 17 detected. Enabled workaround for SOLR-16463
[0.001s][warning][pagesize] UseLargePages disabled, no large pages configured and available on the system.
The Java thread stack size specified is too small. Specify at least 448k
Error: Could not create the Java Virtual Machine.
Error: A fatal exception has occurred. Program will exit.
phy2-ap0 可以手动配置 149信道
phy0-ap0 可以手动配置 36 信道
不是所有信道都支持的
td {
background-size: 100% 100%;
background-image: url("data:image/svg+xml;base64,PHN2ZyB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPg0KICA8bGluZSB4MT0iMCIgeTE9IjAiIHgyPSIxMDAlIiB5Mj0iMTAwJSIgc3Ryb2tlPSJibGFjayIgLz4NCjwvc3ZnPg==");
}解决办法:
sysctl net.ipv4.tcp_syncookies=0
查看:
netstat -nat | awk '{print $6}' | sort | uniq -c | sort -n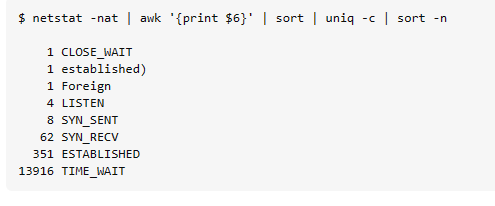
index 924bd51327b7..6841c74eac00 100644
--- a/[Documentation/networking/ip-sysctl.txt](https://git.kernel.org/pub/scm/linux/kernel/git/torvalds/linux.git/tree/Documentation/networking/ip-sysctl.txt?id=39dbc646fd2c67ee9b71450ce172cbd714d4e7fb)
+++ b/[Documentation/networking/ip-sysctl.txt](https://git.kernel.org/pub/scm/linux/kernel/git/torvalds/linux.git/tree/Documentation/networking/ip-sysctl.txt?id=79e9fed460385a3d8ba0b5782e9e74405cb199b1)
@@ -667,11 +667,15 @@ tcp_tso_win_divisor - INTEGER
building larger TSO frames.
Default: 3
-tcp_tw_reuse - BOOLEAN
- Allow to reuse TIME-WAIT sockets for new connections when it is
- safe from protocol viewpoint. Default value is 0.
+tcp_tw_reuse - INTEGER
+ Enable reuse of TIME-WAIT sockets for new connections when it is
+ safe from protocol viewpoint.
+ 0 - disable
+ 1 - global enable
+ 2 - enable for loopback traffic only
It should not be changed without advice/request of technical
experts.
+ Default: 2```
Much appreciated!